Theorems and Related Questions in Isosceles Triangle
Theorems and Related Questions in Isosceles Triangle: Overview
This topic covers Word Problems on Isosceles Triangles.
Important Questions on Theorems and Related Questions in Isosceles Triangle
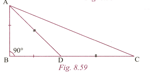
In Fig. 8.59, AB = BD, AD = CD and Find (give answer in degree)
In Fig. 8.57, AB = BC, AD = CD, Calculate (give ans in degree)
In an isosceles triangle ABC, with AC=BC, the line CD bisects AB at D and CAB=. Find CBD.(Give answer in degree)
In an isosceles triangle , with , the line bisects at and . Find (Give answer in degree).
In Fig., , and . Calculate: (give answer in degree)
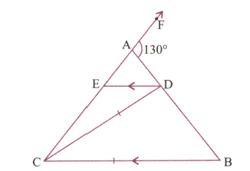
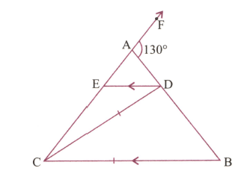
In Fig., AB=AC; BC=CD, BAF= and DE||BC. Calculate: (Give answer in degree)
The vertical angle of an isosceles triangle is . Find each of its angles. (Give answer in degree)
D is a point on the side BC of a such that AB=BD=AD=DC. Show that
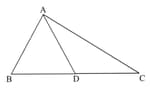
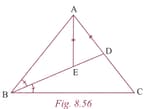
In , and is a point on such that . Prove that .
In a triangle , the bisectors of Angle and angle meet at . If , then prove that triangle is an isosceles triangle.
In figure and Angle angle . Prove that .
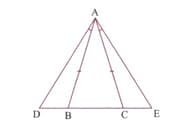
In Figure is such that and is a point on produced. is
perpendicular to produced and is perpendicular to produced. Prove that QS bisects
Show that angles of an equilateral triangle are each.
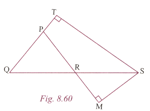
In Fig. 8.58, is an isosceles triangle with . is produced to such that . Prove that is a right angle.
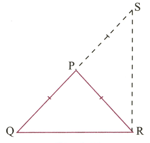
In Fig. is a triangle. The bisector of meets point lies on such that Prove that
If the bisector of the exterior vertical angle of a triangle is parallel to the base, then show that the triangle is isosceles.
In given figure and is the bisector of . Prove the is an equilateral triangle.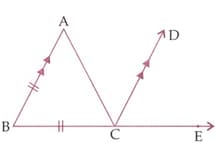
Through any point in the bisector of an angle, a straight line is drawn parallel to either arm of the angle. Prove that the triangle so formed is isosceles.
Two lines and intersect at such that is equal and parallel to , Prove that the lines and bisects each other at .
and are, respectively, the perpendicular to the side and of a . If , prove that is isosceles.
